Start point of an analysis of robust property of uncertain systems by numerical experiment
In this section, nominally linear system with linear or nonlinear disturbance or uncertainty is analyzed with numerical experiment. Theoritically speaking, by my core thesis of M.Phil thesis, it is proved that almost all uncertainty can be estimated and it is utilized to cancel out to hold robustness of a system. However, there are no study for a case of nonlinear disturbancce and why that control signal make a system robust. The ultimate question is numerically, is it really possible to estimate even disturbance is nonlinear? It will be shown that what kind of behaviour is expressed by nonlinear disturbance and estimated disturbance to cancel out by numerical experiment.
Nominal systems considered in this thesis is linear. However, in the real world, nominal system is nonlinear. In further work, it is supposed to analyze nominally nonlinear system. In the theory of linear control, the theory is much rely on linear algebra. If it were nonlinear system? That tool cannot be used. Thus, forget about algebra but think about physics and geometry and relation between algebra and geomery with linear system and physical insignt are considered for the connection with nominally nolinear systems.
Although, nonminal system is linear, feedback control input of the robust control is time-varying signal. Thus, controlled closed loop system is kind of nonlinear system. It could be said that nonlinear system is better for a robustness. If a nonlinear feedbacked system is better than linear system in terms of robustness, it could be said that a control designer think about nonlinear feedback to a system with nominally linear systems. These argument will be investigated in this section.
Also, the following part is open loop response though disturbance is estimated. Study of closed loop response will be done later.
Environment of numerical experiment is as follows:- Programming language: Python (ver. 3.8.x)
- Visualizing tool: Matplotlib
- Solver of ODE: euler method (Runge-Kutta? Author thought that it is not required considering some numerical experiment done before serious analysis).
- CPU: Apple M1 2020
Note that program of the solver of this ODE and observer will not be open source because of considering educational effect. Authour thinks that a student should have technique to implement their own tool of experiment regardless of it is numerical experiment or real experiment.
Why? That is because if one goes to a company or research lab, one is required to make their own tool. Always ask to technician? Ask to technician 100 times per month for their drill down? No it is nonsense regardless of one is researcher or developer.
Here is a hint. Author would say that it is better to study object oriented programming and design pattern. If it were possible, having little knowledge of functional programming is better.
The author changed his mind. The code of solver of disturbance observer is open on github. Why? That is this code could be the base of building block and not general enough. This simulator is specific to 2-dimensional systems and for real situation, it should be extended to higher order systems. It will be remained to work of students. It would make their understanding better and would be their skill. Another point is this solver use technique of object compostition and ordinary students of systems may not much about object oriented programming. It is encouraged to use this code as base and extended. Github URL is https://github.com/khj1977/python_ode .
Nonlinear disturbance with a physics of void in a material
In this section, nonlinear disturbance is analyzed using numerical experiment. In core thesis, it is implied that almost all class of disturbance can be estimated and cancelled out to retain robustness of a system. However, in practice, especially, for hard nonlinear uncertainty or disturbance, is it really possible to estimate? Is there something which lacks in this theory? That question is investigated by this section with nonlinear void disturbance.
f = lambda t, x, xDot: -2.0 * x - 1.0 * xDot
disturbanceF = lambda t, x, xDot: -1.0 * math.sin(t) * x - math.cos(t) * xDot - 2.0 * math.sin(t) * x + 6.0 * math.sin(t)
Where f is ODE. And disturbanceF is disturbance input to the actual system.
Why this disturbance or uncertainty? It is close to parametric uncertainty but its parameter is changed periodically. That is modelling of void or little bit unbonded reinforced region of alloy or CFRP. Using a material long time results fatigue of material and its characteristics may be changed. Since if a system is alloy or CFRP, its dynamics could be represented by Yet Another Mori-Tanaka, this supposition may be correct. In addition sin(t) is a toy of vibration or force of wind to a material.
X0: x0: 10.0, xdot0: 5.0
T: 0.0:10.0, deltaT = 0.01
U = 3.0 * x1 + 15.0 * x2
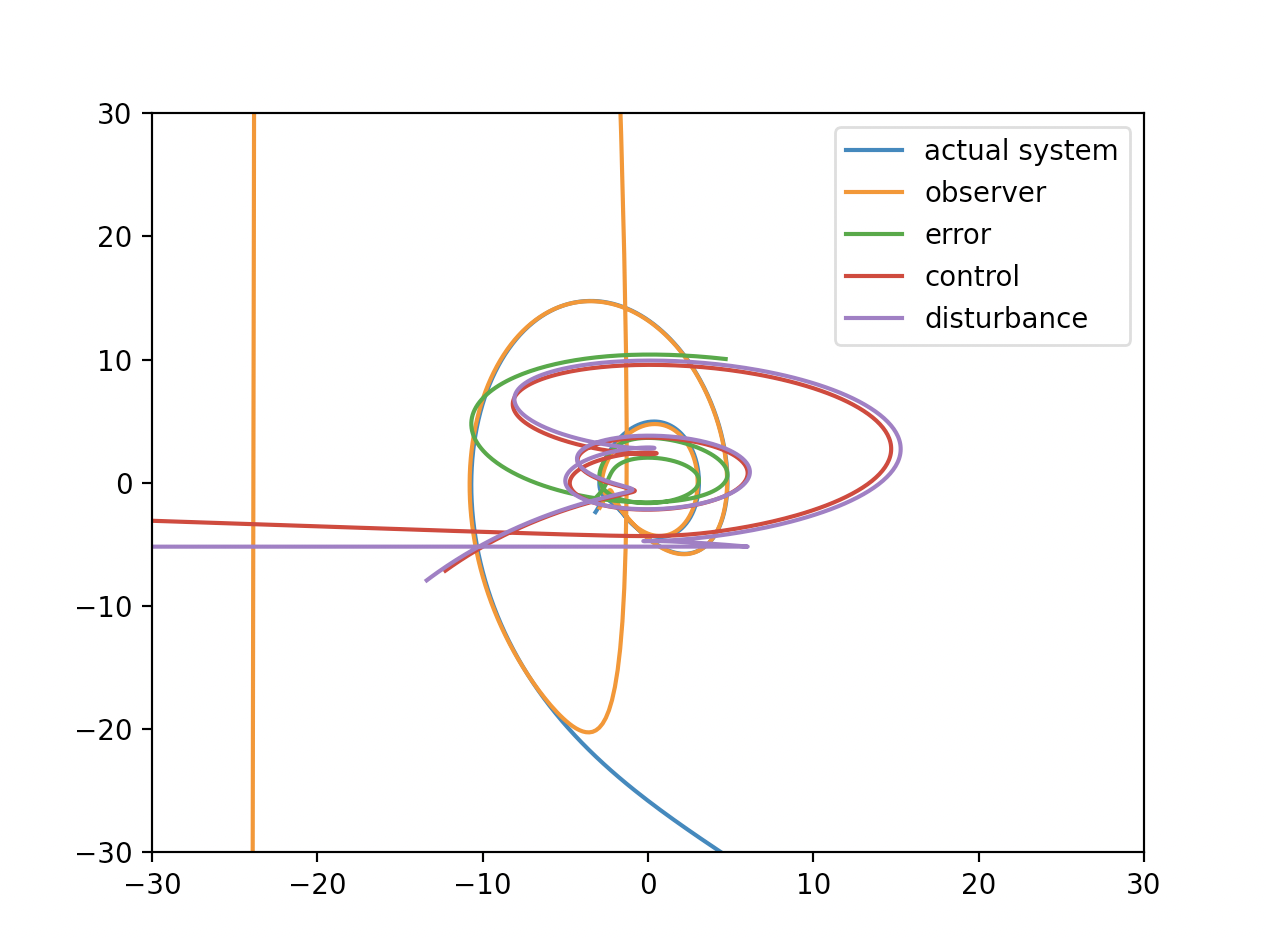
Where x axis is xdot and y axis is x. Nominal system is periodical but converges to origin. Transient response of observer is not good. Is it because of gain of observer or bug of program?
Disturbance is estimated well. But there is error. That might be because of fact that gain is not appropriate. If it were adaptive, it is OK.
Nominal system is linear. But disturbance is nonlinear with sin pure disturbance. It makes system interesting behaviour. It is better to make endT longer and check basic data. And drill down.
It might be better to change range of x-y of grpah to drill down with the same time range.
It is better to check data with t-x and t-xdot axes to check how it oscialate from the other view point. Heat map would be better choice to check behaviour of tangent space since overall system is nonlinear. But it will require much more CPU power and hence, it might be little bit difficult though it is worth to investigate it.
t: 0:100.0. deltaT = 0.01
With the same parameter as above.
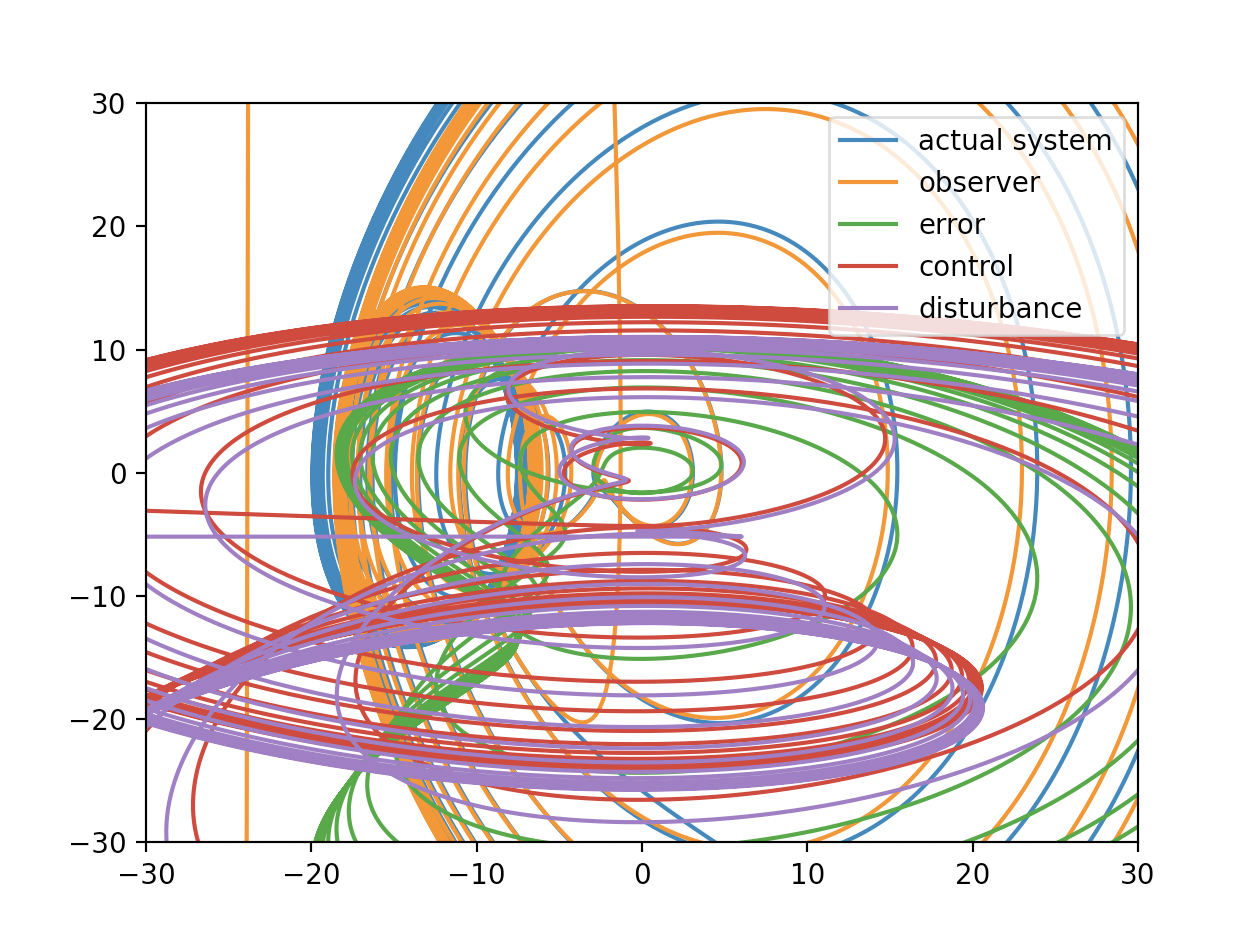
There is effect to nonlinear disturbance to actual sytem which is oscilating. Very interesting behaviour with nonlinear. It would be interesting to analyze modes of this dynamics using FFT. Does this dynamics become chaotic?
A question is, Is it possible to estimate disturbance perfectly with adaptive feedback?
It could be supposed that if it were wing of aeroplane, its behaviour cannot be tolerated since it is used to control dynamics of fluid and aeroplane itself. Or even wing could be broken. Thus, control is required.
The dynamics of fluid is modelled by sin(t) but in practice, it would be more complex signal. If there are hard disturbance, it would be difficult to control behaviour of aeroplane. Cancel out its behaviour using K-Disturbance Observer is one of a way. But if a dynamics of fluid is partially controllable with some change of shape of wing of aeroplane, what would be happened? If fluid were modelled by Digital Langrangian, it is high order ODE and it is targe of control. In that time, sin(t) is a subsystem to be connected to a main system. It would be obvious to specialist of fluid dynamics. But for author, it is interesting topic to investigate.
Although author is not specialist of econimist, there is one thing to mention. Decoupling of a sub system would be a topic to dynamics of economics. But decoupling would require much more control input. So, it is better to utilize more effective control. Sometimes, sliding mode or disturbance observer is good for economical system. But for sometimes, ordinally control is better to that kind of system. Author would like to know investigation by economists.
Using theroy described in my core M.Phil thesis, it is possible to estimate void of a material during it is under opereration. If there could be void, it should be maintenanced or even exchanged with new one. But since it is sensored by attached material, measurement itself could be broken. Hence, it can be said that measurement and mentenance on offline is important.
Although it would be obvious for specialist of economics, there is small mention about dynamics of economical system from a view point of control. Forgot about inter-country effect. Then, a system of a country will be some kind of matrix A where it is linear or nonlinear. State would be a topline of a industry or even a saraly of a person.
Author suppose that Japanese economy is not good state because there would be some non appropriate balance of expense of personal budget. Provided that, a problem of optimization of Japanese economy would be optimization of state dynamics. Then, what would be done would be re-design of system matrix A of Japan possibly with control.
Note that for economists, it might be difficult to mdoel a system by matrix A and vector x. But it is better to model by graph;i.e. node and edge graph. Then, covert that graph to matrix A where it would linear or nonlinear matrix.
Why such a remark? That is because author is writing MBA thesis: The Modern Strategy from Japan (in Japanese). That thesis is for turn around of Japan.
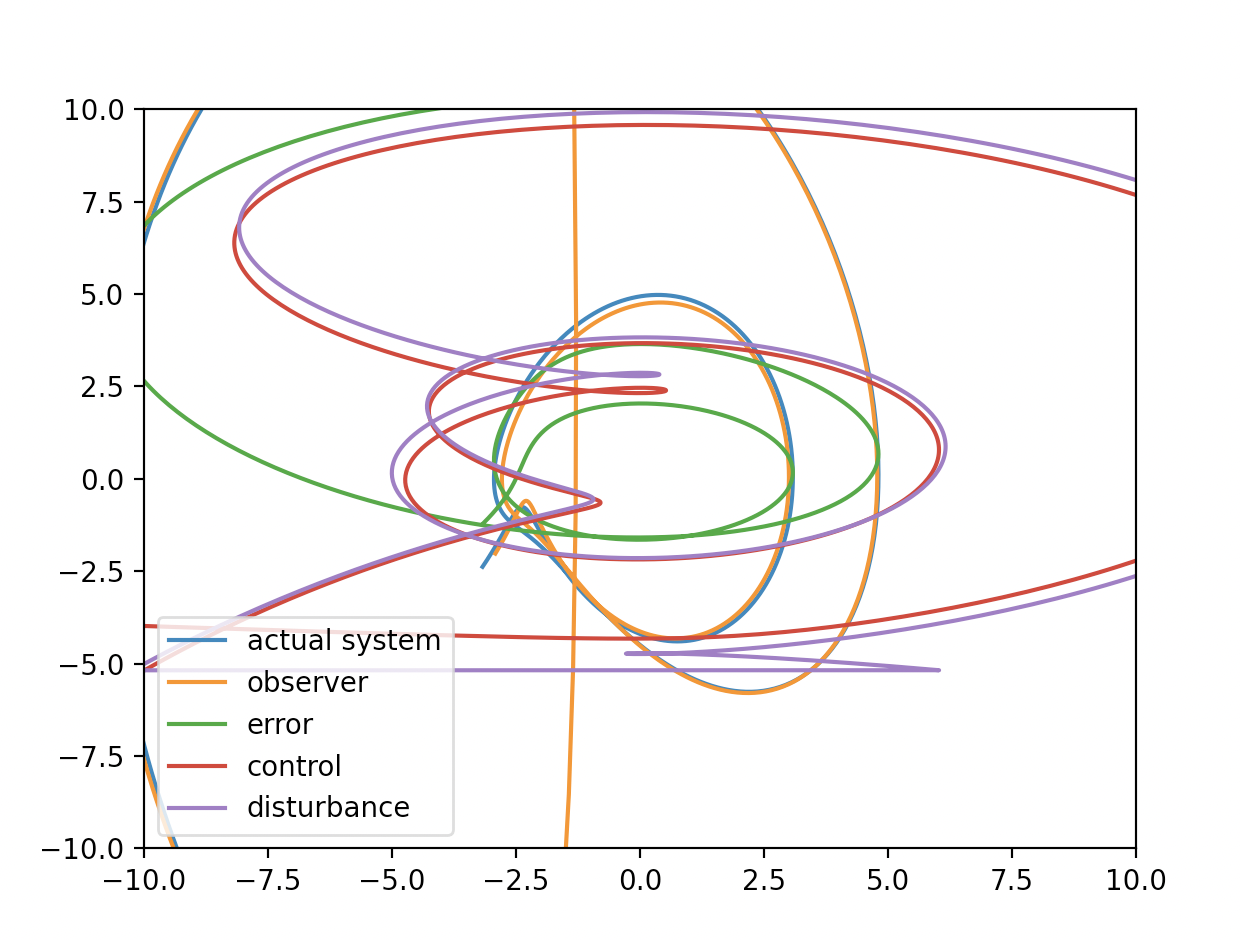
Range of graph is changed. There are error between oberver and actual system. There is error with disturbance estimation. It might be because of gain of observer. Since the nominal system is linear, if perfectly nonlinearlity is cancelled out, it should ocsilate around origin or stable around origin. It means that even nonlinear effect with modelled one is cancelled out, in practice, it could be still nonlinear if no robust control is applied. Actually, in the field of CFRP which is done at University of Tsukuba, there is a modelling error with nonlinear experiment whose model is complex enough. In this part, estimated disturbance is not used to cancel out. It might be interesting to see what will be happened if it were used to cancel out. It would be still nonlinear. Does it go to delta region? It should be investigated later.
Closed loop response with adaptive feedbacked nonlinear disturbanced system with a physics of void in a material
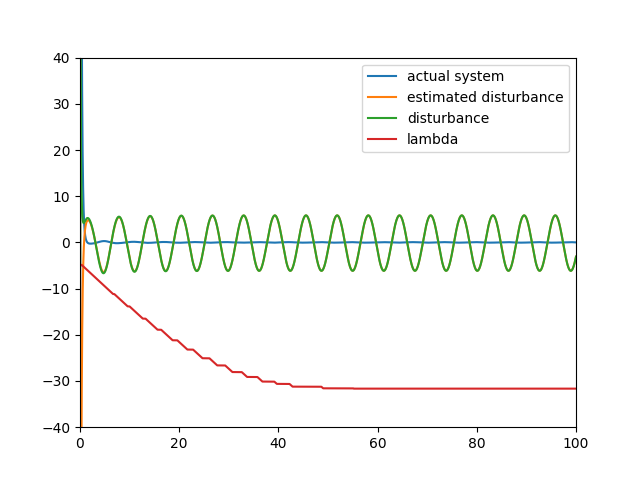
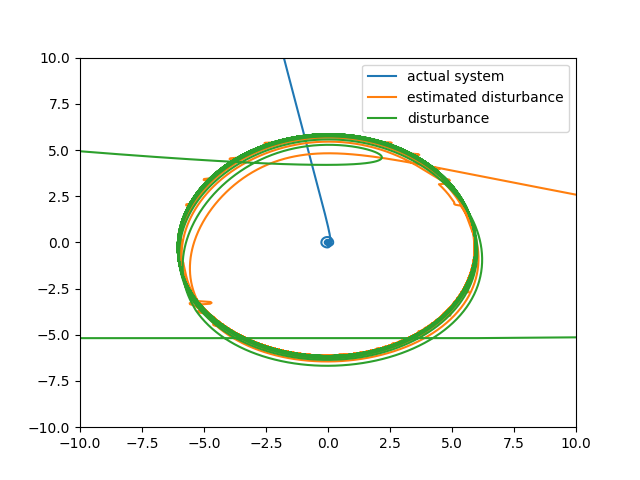
Now, adaptive robust control with feedbacked system. Adaptive feedback disturbance estimation work well even it is fedbacked to actual system. It proves that even disturbance is nonlinear, this control method works well.
Actually, it could be said that assumption of disturbance f(t, x) for analysis and proof does not think a detail of nonlinear function f_nonlinear(t, x) and it might not be work for nonlinear disturbance but as proved by this numerical experiment, it works in this case. If nominal system is mixture of linear and nonlinear system, one way to control is to cancel out nonlinear terms. In that way this control method can be used. It is clearly seem in this numerical experiment result.
One thing it should be mention is this numerical experiment does not cover all nonlinear effect. The question at this time is, is it possible to cover all kind of nonlinearity? It is not possible to by numerical method.
However, major objective of this thesis is to imply for typical nonlinear effect would be possible to cover by this k-disturbance observer. And thus, it is said that this adaptive robust control method can also be used for nonlinear systems.
The remaining topic is nominally nonlinear system and how to guarantee robustness of that class of systems. Linear algebra? Eigen value/vector? It cannot be used for nonlinear system. Forget about algebra. Rather, geometry is used to understand nominally nonlinear system. To understand system geometrically, linear systm with different characteristics are used since it can be understood via linear algebra. In addition, to understand what is a robustness, analysis of signal which stabilize systems geometrically will be utilized.
Conclusion of adaptive feedbacked robust controlled systems
By those figures, it can be said that with appropriate feedback gain to disturbance observer, it can be estimate disturbance very well. As pointed out by other researchers, weak point of my core M.Phil thesis is definition of disturbance function f(x). That is fine to estimate parametric uncertainty by observer. But if it were hard nonlinear, is it still possible to estimate nonlinear disturbance well? An answer is affirmative. By numerical experiment, it is shown that it is possible to estimate and canceled out for some cases.
It could be said that the analysis or thought of what is disturbance and uncertainty, which is f(x), was shallow for my core M.Phil thesis. But as said, the remaining point is to think about characteristics of nonlinear effect f_nonliner(x, t) regardless of analysis or numerical experiment. Since, it is not possible to analyze all class or even one class nonlinear effect, as shown in this section, it is better to analyze by numerical experiment.
As pointed out, even nonminal system is considered as linear, there would be hidden nonlinearity. It means, one developer makes controller based on linear nominal model, that system would not work well but nonlinear behaviour would be remained. The same thing is also said to feddbacked linearized systems, since there are unmodelled nonlinear dynamics. So, nonlinear disturbance is important. It is partially proved that even hard nonlinear, disturbance is estimated well. If it were adaptive, estimated disturbance would be better than this one. Note that it could be said that all the class of nonlinearity cannot be proved to be estimated. But practically speaking, numerical experiment of some class of nonlinear disturbance would be enough. The theory and proof of all the class of nonlinear disturbance is left for further work.Since a nonlinear disturbance or uncertainty can be tracked and estimated, disturbance function f(t, x) could be any or some kind of nonlinearity. It implies that with the stable linear nonminal system A, even overall system is nonlinear, a system can be controlled robustly using this robust feedback controller.
Therefore, the adaptive feedback controller proposed would be usefull for practical situation. If there are no input constraint and a user of controller does not chase myth of nonlinear, it could be said that this adaptive robust controller is one of the choice for engineer for smart material systems or even for robot.
Yet another question is, is it really required to cancel out all the uncertainty especially nonlinear effect? Actually, since contorller is designed based on nominal system, it is better to cancel out disturbance. That is the objective of controller of this thesis and research. However, if there exist nonlinear system which is robust even there is uncertainty and converge into delta region, it is not required to cancel all the effect of disturbance. Since there is input constraint it would be better to research quasi robust property of nominally nonlinear system.
If this supposition is correct, it would be better to research nonlinear feedback controller even for nominally linear system especially for robust control.
Sometimes, in journal papers, research of control engineering is research of control engineering. That could be OK. However, the author would like to take the strategy to start to research nonlinear control from systems dynamics. Because if behaviour or characteristics of a system is known through research of systems dynamics, "why" is known, and then, naturally, new kind of nonlinear controller could be made. Rest of work could be research of systems dynamics both for linear and nonlinear systems.
Geometrical analysis of nominally linear systems
From this part, nominally linear system is analyzed. Although dynamical behaviour of nominally linear system can be evaluated by eigen value/vector of a system matrix A, geometrical analysis is deployed in this part. That is because of fact that if a nominal system is nonlinear, linear algebra cannot be used anymore expect analysis on tangent space of manifold. Therefore, for nominally nonlinear system, firstly, linear system is analyzed geometrically, and then, nominally nonlinear is analyzed mainly by geometrical aspect using the insight of combination of algebra and geometry of nominally linear systems. Moreover, insight of physics would be deployed to use analysis of dynamics since author would say that if it were physically correct, it would be mathematically correct.
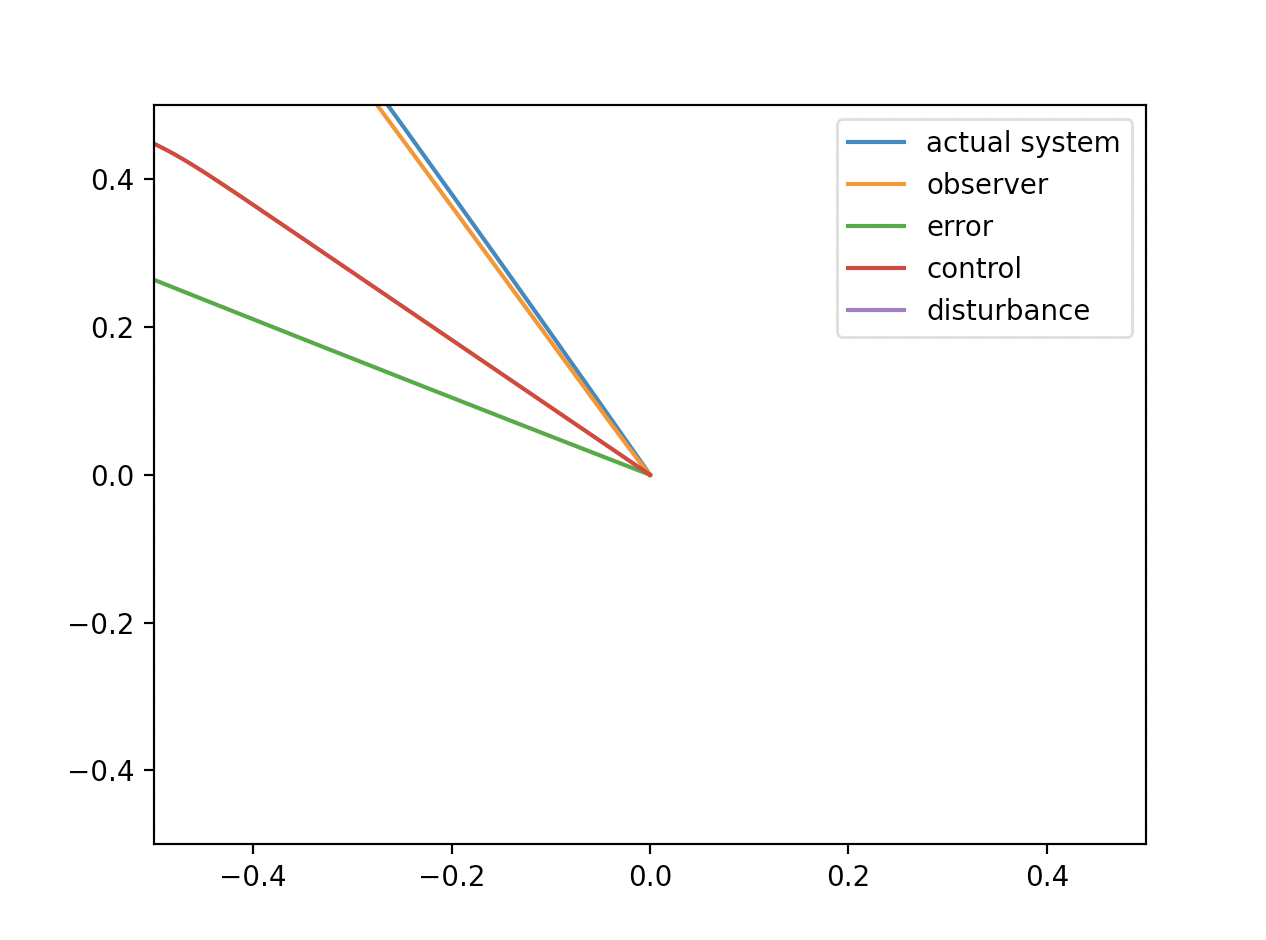
f = lambda t, x, xDot: -6.0 * x - 5.0 * xDot
disturbanceF = lambda t, x, xDot: 0.0
T: 0:100.0 deltaT + 0.01
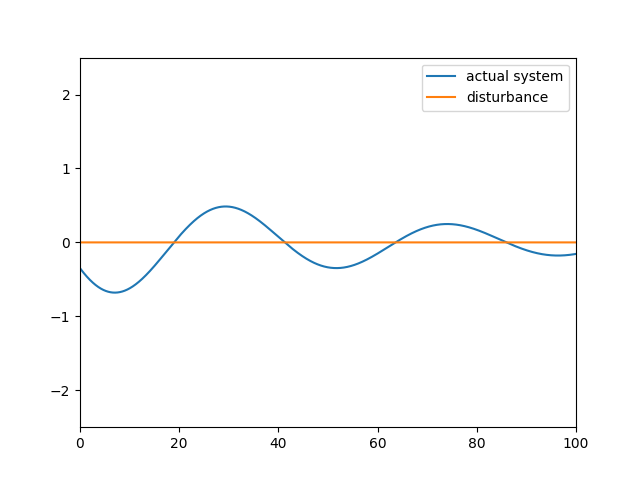
Without disturbance with nonminal system is stable around origin. It converges to origin appropriately
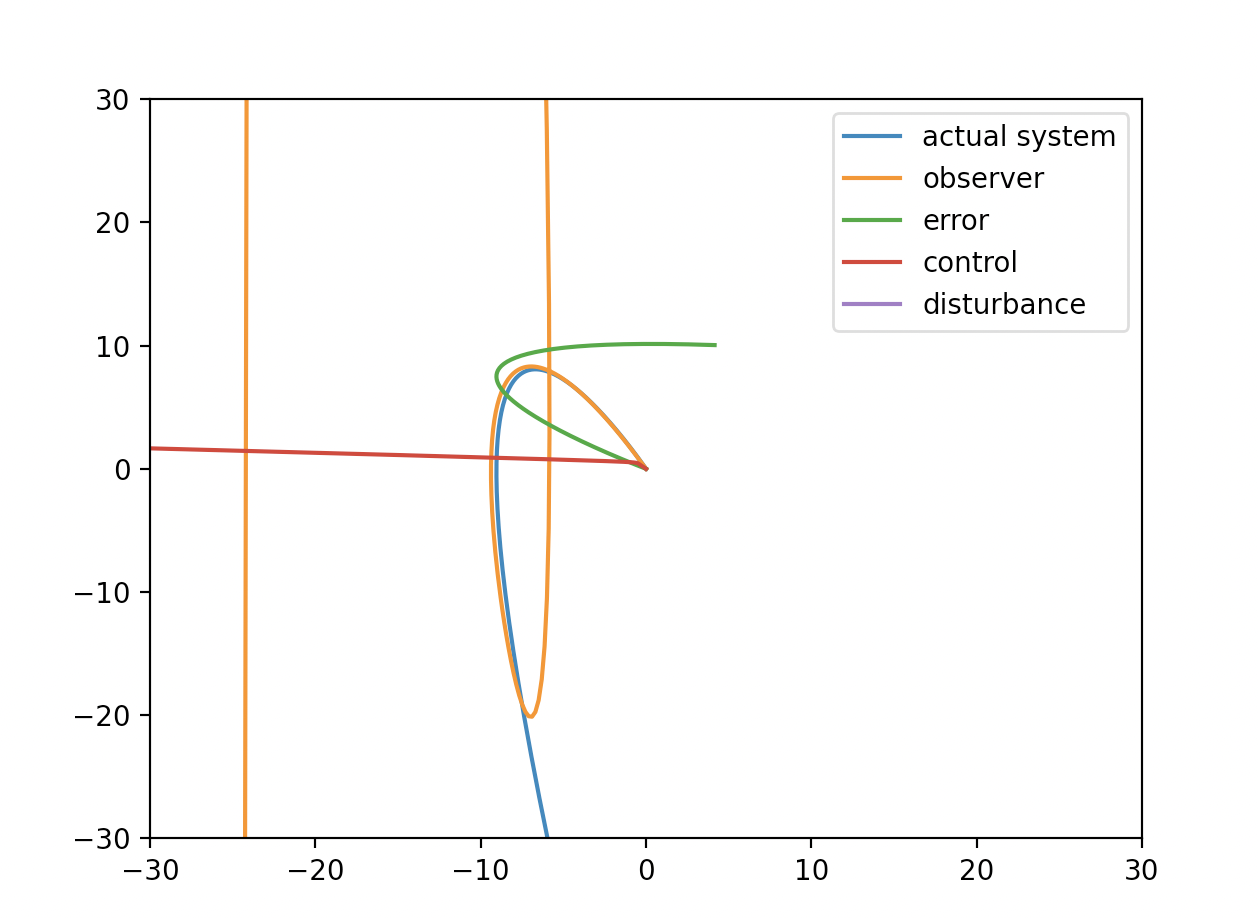
The same setting with above. Transient response of observer is not good. But it converges to actual system well. Since nominal system is stable, it converges to origin well.
There is little curve of trajectory of actual system.
X is little bit over shoot. But not so wrong. There may be better transient response and parameter of nominal system. It is required to change behaviour of system by feedback.
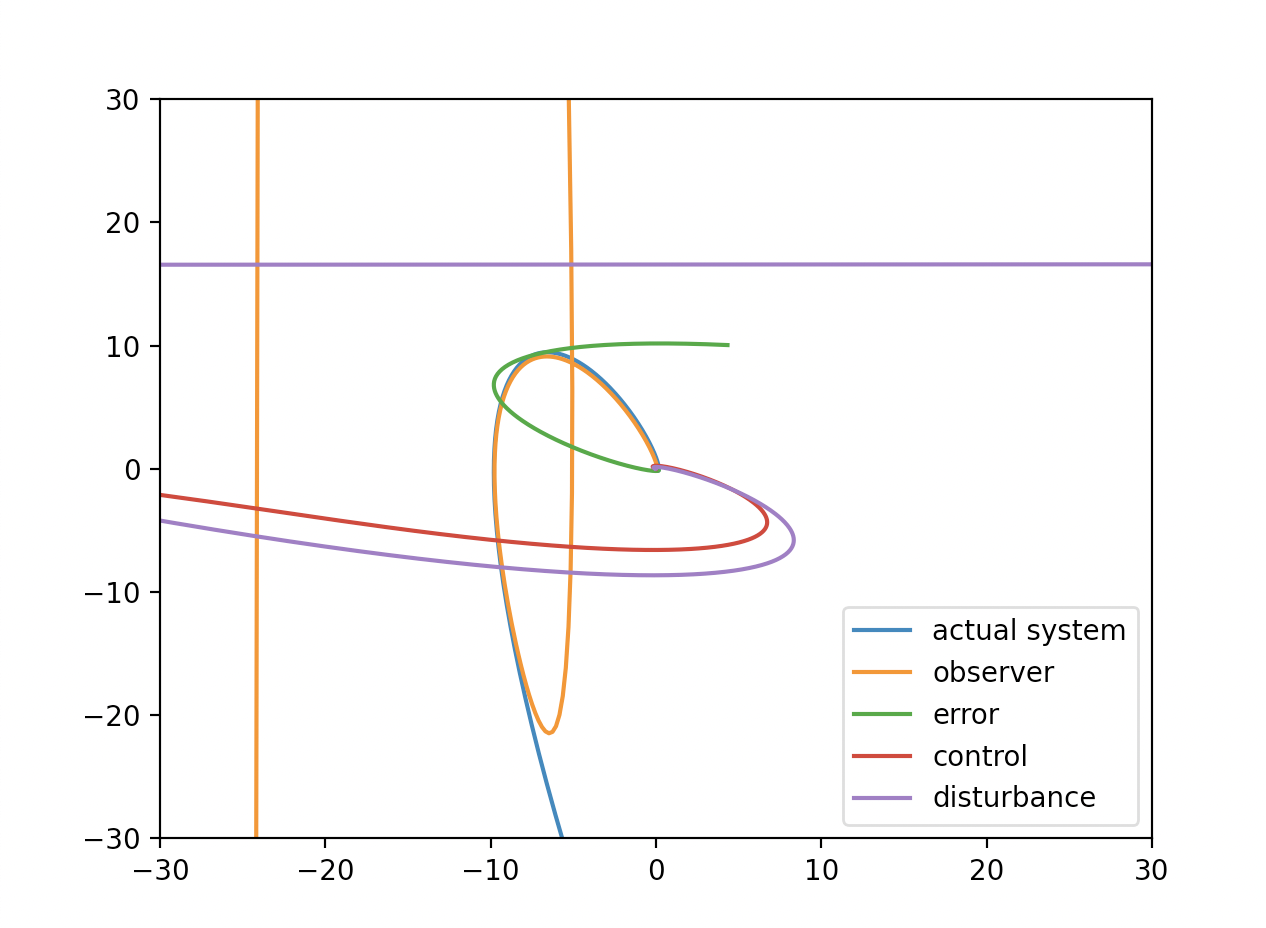
f = lambda t, x, xDot: -6.0 * x - 5.0 * xDot
disturbanceF = lambda t, x, xDot: 1.0 * x + 1.5 * xDot
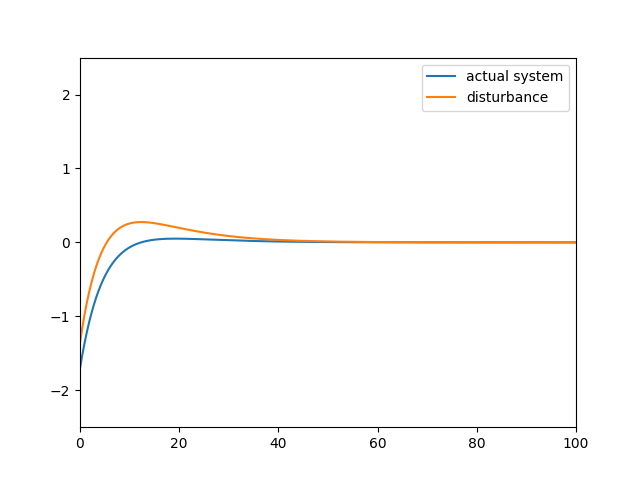
The nominal system behave well. There is error of estimation of disturbance but it does not result bad result. Transient response of observer is a problem. What is happened if as a result of disturbance, the system is unstable? Is estimation speed of feedback is fast enough to stable system?
Test the same disturbance with 0 feedback of estimation of disturbance.
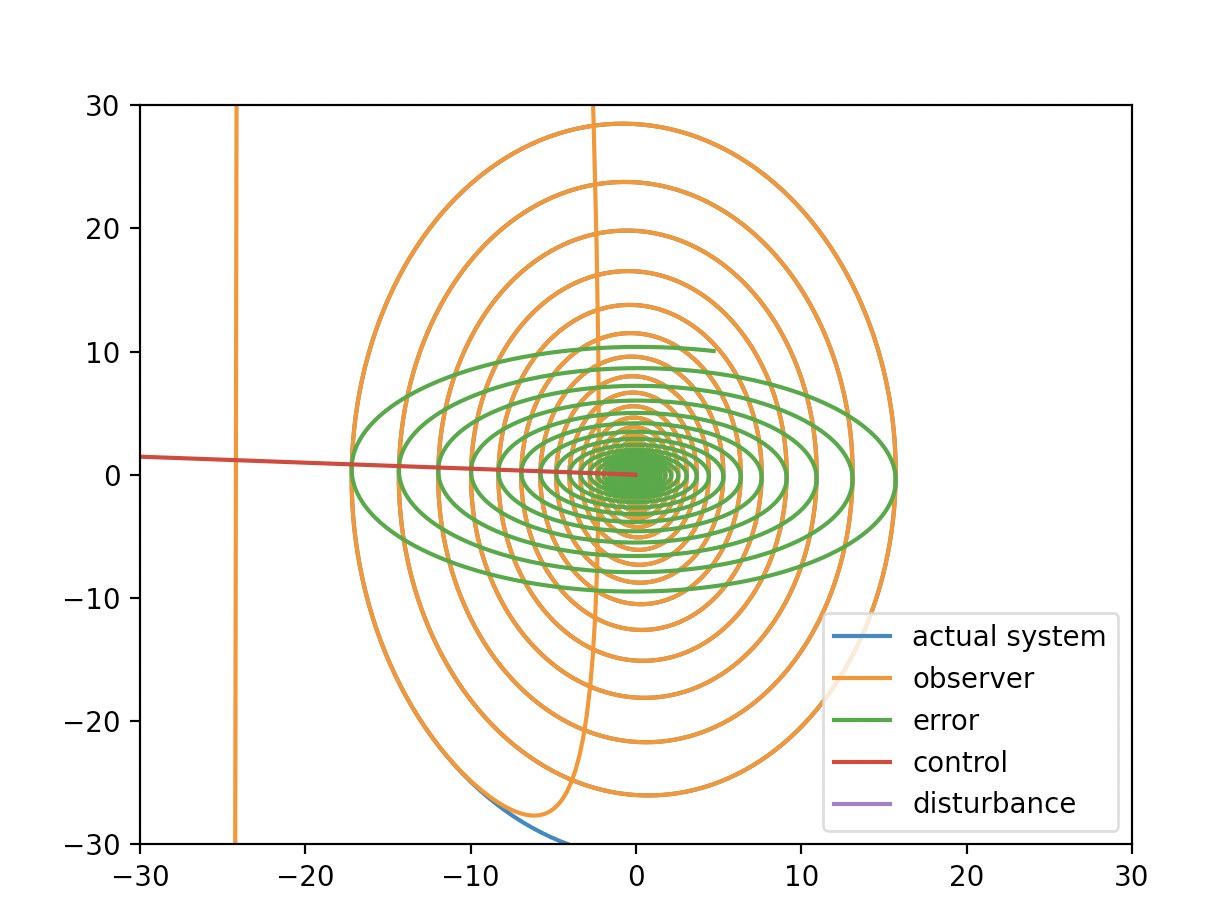
f = lambda t, x, xDot: -3.0 * x - 0.1 * xDot
disturbanceF = lambda t, x, xDot: 0.0
Since the effect of linear spring is strong and little effect of linear dumper, it osciallating but converges slightly with wave. Because dumper absorb energy of the system, it converges to the origin. The question at this point is if there is a nominally nonlinear system and nominal system does not converges to equibrium, using linear dumping feedback control make system stable around origin? What happened if nonlinear dumper is used for control of nominally nonlinear system?
Also, nonlinear disturbance described in the another section, - math.cos(t) * xDot, seeems to change the mode of system since coefficient is -cos(t). Is coefficient of dumper xdot^2? It means the system is xDot^2 * xDot?
Note: why nonlinear dumper is xDot^3? Author supposes that might be the same reason with effect of pressure of wind against fast vehicle or bicycle. If it were wind, if speed gets faster, its wind pressure gets higher. It is not linear. So, considering fitting with pressure curve, it would be xDot^2 or xDot^3.
Or even there could be another type of nonlineaer dumper which is x * xDot. Or even it could be sum_i(delta_i * sin(omega_i * x)) * kappa * x * xDot. Why? As for x, that is because an effect of a absorber may be depends on its depth within an absorber. Also, sin(omega_i * x) expresses a effect of turbulence of fluid dynamics of oil with moviing absorber. It is very interesting modelling. It would be investigated later.
It should be noted that if characteristics of nonlinear dumper gets clear, it could be possible to make nonlinear feedback controller. So, the yet another question is what is an appropriate control input? In the sense of asymptotic stability, robustness and optimal control. It would be different respect with an objective. At this time, since robustness is the main topic of this research, author would investigate with the view point of robustness.
It is said in this part that in analysis of nonlinear nominal system, physical insight and comparison with linear counter part will be deployed to analyze its dynamics. If it were linear, it is obvious that it can be analyzed by eigen value. But if it were nonlinear, it can not. Is there some view point which describe what is nonlinear completely? No, there is not. So, using hypothesis driven physical insight, some technique of visuallization and numerical and analytical mathematical analysis, which is not formula like eigen value, will be deployed.
If real world applications are nonlinear and linear algebra is obsolete, studying linear algebra is not required? The answer is no. If it were mechanical systems, it could be analyzed using taylor seriese by each (t, x) of a system xDot = f(x, t). If it were NLP, there are many real world application of linear algebra. If it were psychology, without knowing linear albebra, statical processsing cannot be done. In that sense, linear algebra is still important.
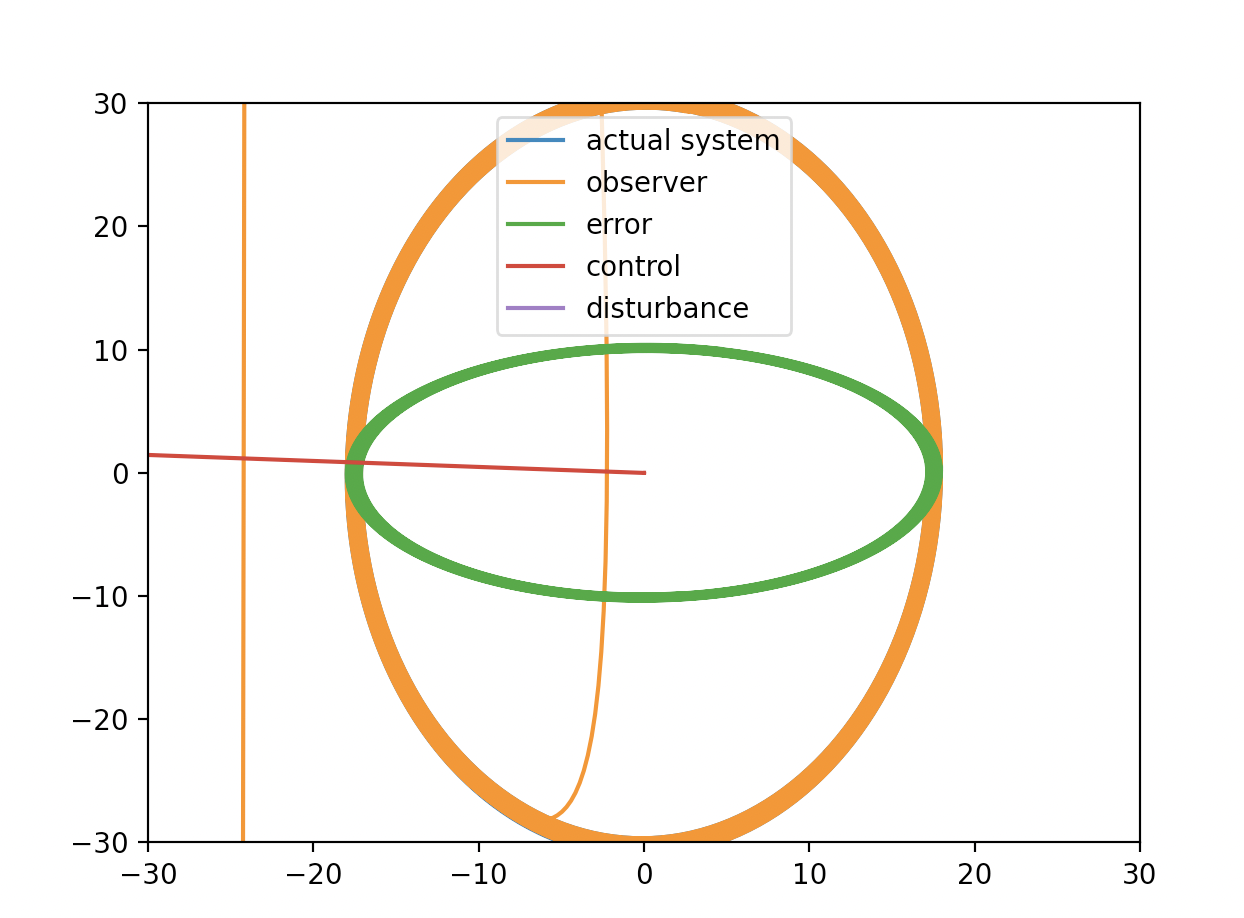
f = lambda t, x, xDot: -3.0 * x - 0.001 * xDot
disturbanceF = lambda t, x, xDot: 0.0
Since the effect of linear dumper is too small, the system is almost oscillating.
However, error dynamics is too large despite the fact that trajectory of disturbance observer and actual system seems close enough. Or it is not close enough? Just it is not analyzed by drill down? It is odd because other ODE trajectories seems fine.
There could be bug of program. The question is if there was bug, these numerical experiment is obsolete? The answer is no. It was sugtested by a researcher that if bug is analyzed, and that effect of error is included in nominal system or disturbance, this research result is still fine.
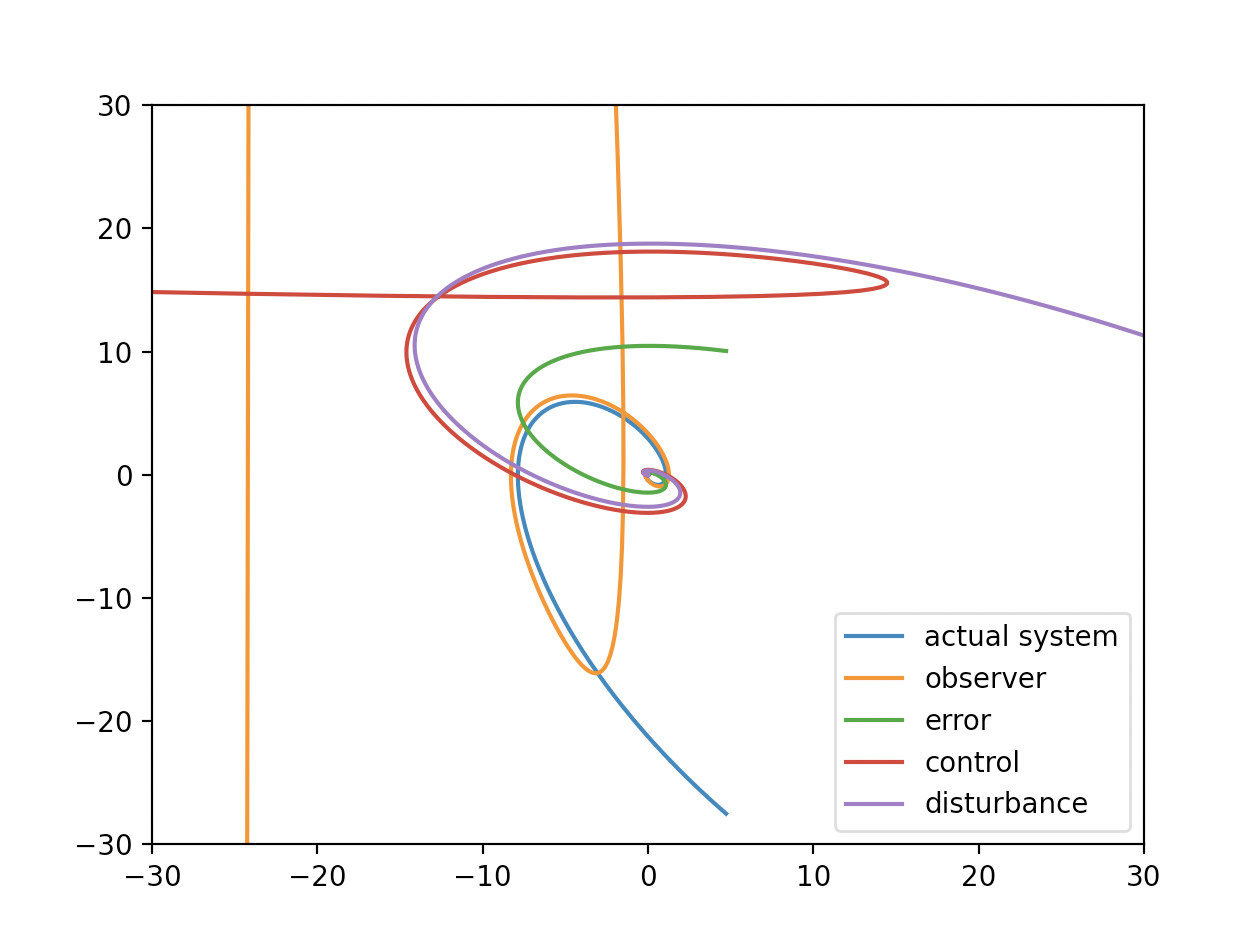
disturbanceF = lambda t, x, xDot: 1.0 * x - 1.5 * xDot
Disturbance is dumper. The system becomes stable around origin but dumped. What will be happened if trajectory is shown around origin?
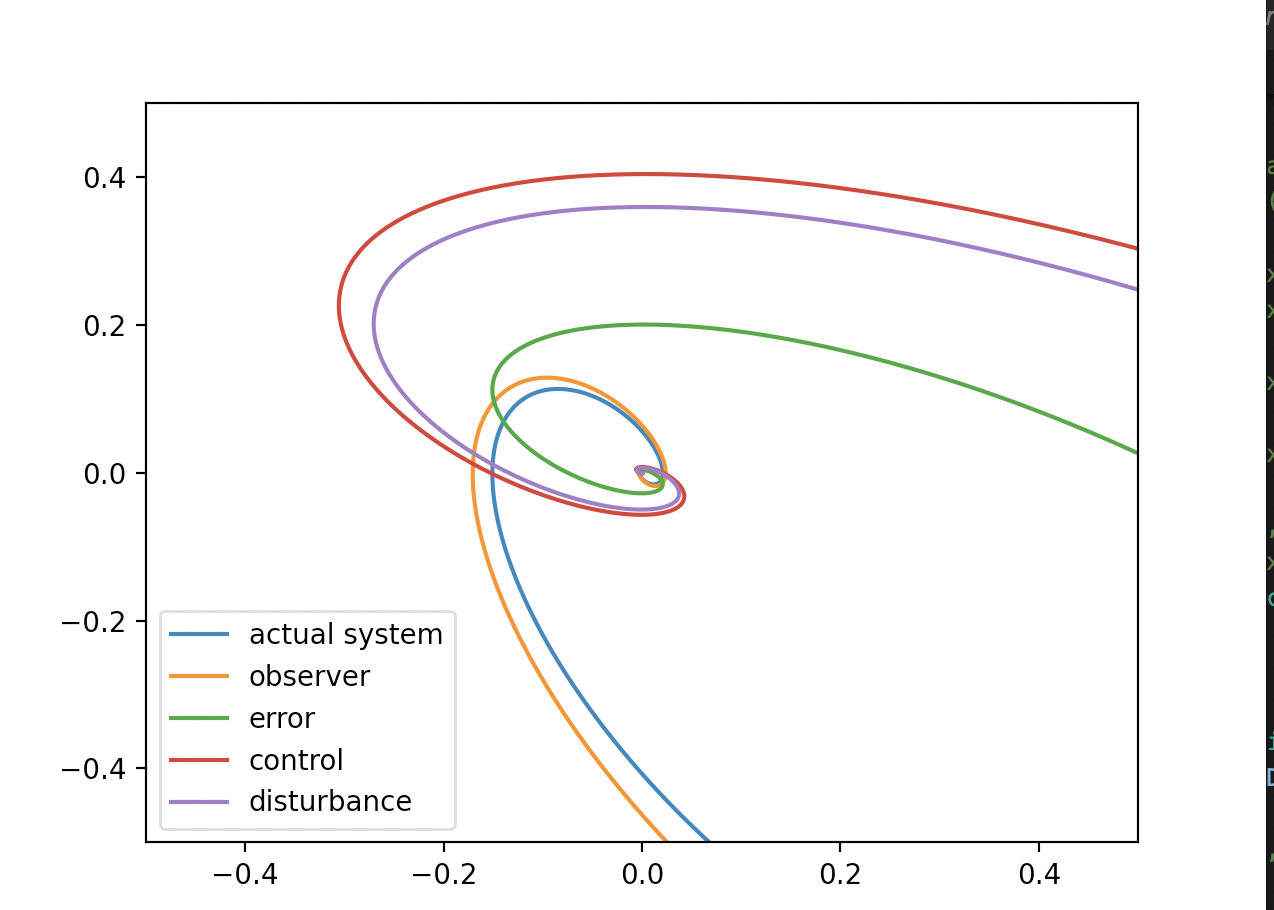
It oscialte with the effect of dumper as disturbance. What if gain of disturbance observer is determined adaptively? The current gain of observer is as follows:
U = 3.0 * x1 + 15.0 * x2
It seems the error between estimated disturbance and actual disturbance is small enough. But the system is oscillating around origin. System will goes to delta region, so small behaviour in delta region may exist. It may cause disturbance oscilate. The question is the same. What happened if the gain is determined adaptively? Then, oscilating gets small enough, and it would be tolerant for actual system such as robot, vehicle or even building. Note that the nominal system is not stable but osicillating roundly around origin. The effect of nominal system make that system behaviour?
However, since it is delta region, it could be OK for this dynamics.
Trajectory and characteristics of control input for linear nominally nonstable system -What kind of control input system stable?-
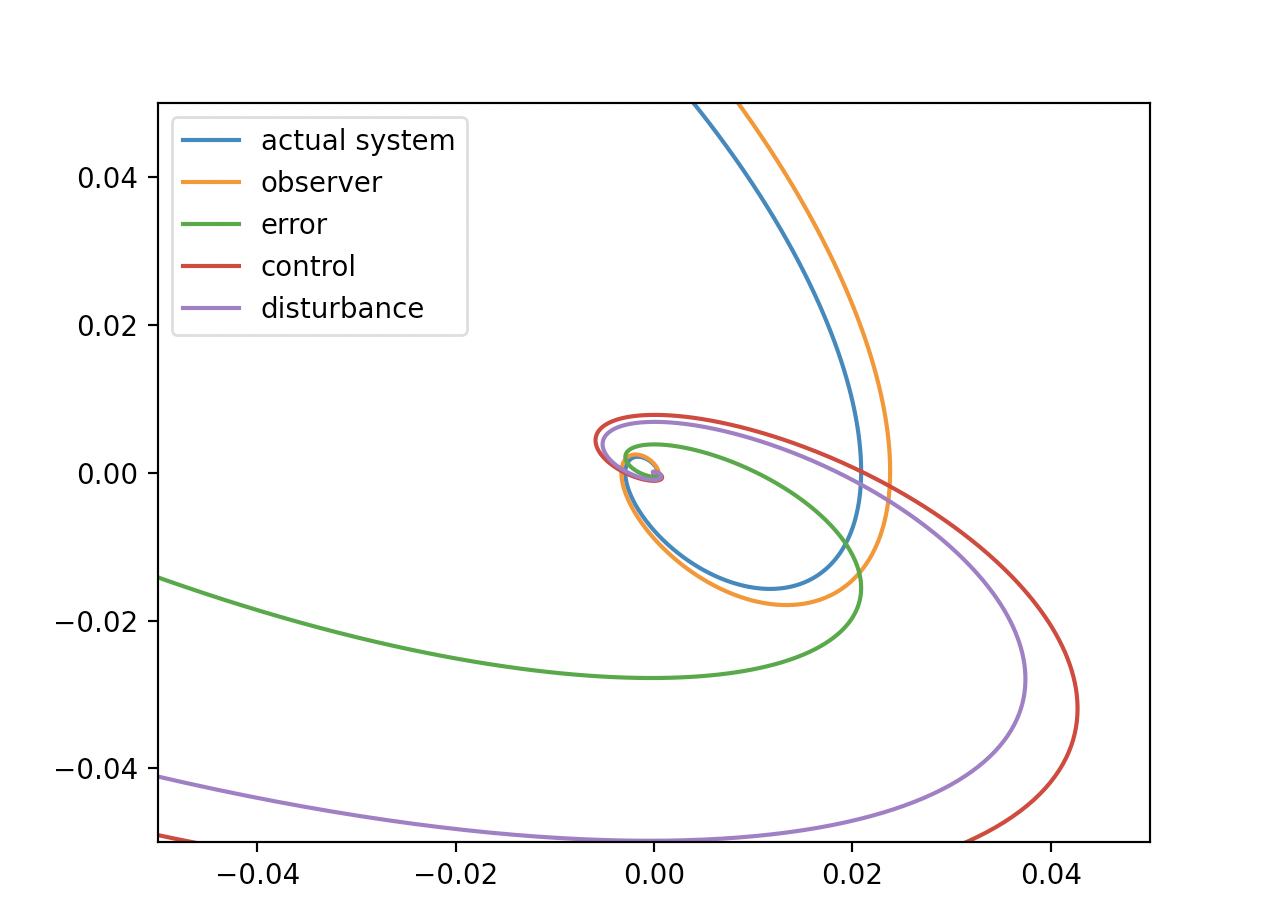
f = lambda t, x, xDot: -0.02 * x - 0.03 * xDot
Closed loop. Feedbacked to make system stable.
Control signal: disturbanceF = lambda t, x, xDot: -0.27 * xDot
Control signal is not inverse of trajectory of open loop actual system. Which implies that control signal or robust control signal could not necessary to be signal to cancel out behaviour of nominal actual system which is disturbed.
Or even control signal makes system goes to equibrium and no signal is not required if it were zero dynamics at equibrium since all dynamics could be zero or x and xdot is zero.
If disturbance is purely depends on time t, which is like sin(t), it should be canceled out. But if it were depends on x, it could not to be canceled out but manipulate vector field, and then, it could control a system, robustly.
Disturbance signal d(x, t) could be estimated by the method made. Then, it could be better to estimate model in that signal d(x, t) and then, to make control signal online may be better choice to control robustly.
Actually, this robust control method can be used for even nonlinear disturbance. However, the author has interest what is a nonlinear system not just control.
Conclusion remark
The author's hypothesis is that there would be nonlinear control feedback which makes robust for change or affect of vector field to nominal system, not by just cancel out the uncertainty or disturbance. Analysis of visualizing vector field and lyapnov function like value considering geometory may be the point. Thus, at further work, this issue would be tracked.